Игнатьев М.Б., Санкт-Петербургский государственный университет аэрокосмического приборостроения, профессор, д.т.н.,заслуженный деятель науки и техники РФ, лауреат Государственной премии СССР и премии Президента России, директор Международного института кибернетики и артоники в Санкт-Петербурге, автор свыше 500 книг, статей и патентов
КИБЕРНЕТИЧЕСКАЯ КАРТИНА МИРА
Успехи современной науки со времен Ньютона неоспоримы, но чем энергичнее внедряются ее результаты в виде различных машин и технологий во все сферы жизни, тем явственнее проступают ее недостатки. Один из главных недостатков заключается в том, что современные технологии рассчитаны на использование больших количеств энергии и материалов, на использование больших давлений, напряжений, усилий, температур и т.д., что приводит с загрязнению окружающей среды, исчерпанию источников энергии и материалов, гибели живой природы – то есть к тому, что называют экологическим кризисом.
Истоки этих недостатков лежат в самой парадигме современной науки, ее деятели слишком часто пользовались бритвой Оккама, срезая как бы все лишнее и слишком упрощая проблемы. В итоге сложилось стремление к «гениальной» простоте, физика заполнилась формулами из трех букв вроде закона Ома. И если это было простительно в докомпьютерный век, то с появлением мощных компьютеров, которые буквально входят в каждый дом, неоправданное упрощение недопустимо, недопустимо пренебрежение тонкими сущностями. Информатика имеет дело со слабыми сигналами, которые могут управлять большими процессами. Слабое человеческое слово способно приводить в действие мощные армии. Информатизация всех отраслей человеческой деятельности – это прежде всего выявление возможностей управления с помощью слабых сигналов, слабых по мощности, температуре, напряжению.
Но для того, чтобы управлять системами, необходимо иметь новые модели различных процессов, в сами эти модели должна быть заложена возможность информационного управления. В этом сущность процесса информатизации. Обычно под информатизацией понимается процесс внедрения новых информационных технологий, прежде всего компьютерных и телекоммуникационных, в различные сферы социально-экономической жизни, но этого недостаточно. Люди в основном пользуются моделями 19 века.
Ниже в статье рассматривается новый класс моделей. Любая отрасль науки опирается на модели реальных процессов, в одних отраслях науки эти модели более, в других менее формализованы, но все они используют естественный язык. Естественный язык – это мощная моделирующая система, созданная усилиями всего человечества, очень важно разобраться, как работает эта моделирующая система. Из-за особенностей голосовой и слуховой систем человека естественный язык – это линейная последовательность слов, в которой обозначаются слова, а их смыслы подразумеваются.
МОДЕЛИРОВАНИЕ ПЛОХО ФОРМАЛИЗОВАННЫХ СИСТЕМ
Теория должна помогать решать еще нерешенные задачи, важнейшей из которых является моделирование плохо формализованных систем. Чтобы превратить различные научные изыскания в технологию, необходимо осуществить большую работу по формализации. Вначале человек формулирует свои мысли на естественном языке Ячел , описывает ситуации и задачи на естественном языке, потом, если удается, строит математическую модель, формулирует задачи на языке основных соотношений Яос , потом эти формулировки переводятся на тот или иной язык программирования Япр , потом разработанная программа реализуется в компьютере на языке конкретной машины Ямаш , и как результат решение задачи выдается на языке результата Ярез в виде таблиц, графиков, текстов, анимаций и т.д. Ниже показана вся цепочка преобразований.
Ячел → Яос → Япр → Ямаш → Я рез
Главная проблема – как перейти от описания на естественном языке к описанию на языке основных соотношений. Для решения этой проблемы предлагается использовать лингво-комбинаторное моделирование плохо формализованных систем, которое базируется на использовании ключевых слов, основных понятий, сложившихся в предметной области. Модель состоит из трех групп переменных – характеристик основных понятий, изменения этих характеристик и структурированной неопределенности в эквивалентных уравнениях, которая может быть использована для адаптации и управления. В качестве примеров рассматриваются модели атомов, города, организма и атмосферы.
1. Лингво-комбинаторное моделирование
Лишь для небольшого числа реальных систем имеются математические модели. Прежде всего системы описываются с помощью естественного языка. Предлагается способ перехода от описания на естественном языке к математическим уравнениям. Например, пусть имеется фраза
WORD1 + WORD2 + WORD3 (1)
В этой фразе мы обозначаем слова и только подразумеваем смысл слов. Смысл в сложившейся структуре естественного языка не обозначается. Предлагается ввести понятие смысла в следующей форме
(WORD1)*(SENSE1) + (WORD2)*(SENSE2)+(WORD3)* *(SENSE3) = 0 (2)
Будем обозначать слова как Аi от английского Appearance, а смыслы – как Еi от английского Essence. Тогда уравнение (2) может быть представлено как
A1*E1 + A2*E2 + A 3*E3 = 0 (3)
Уравнения (2) и (3) являются моделями фразы (1). Если мы имеем математическое уравнение F(x1, x2, x3 ) = 0, то можем получить форму (3) посредством дифференцирования этого уравнения, тогда Аi будут частными производными, а Еi – производными по времени от переменных.
Эта модель является алгебраическим кольцом и мы можем разрешить уравнение (3) либо относительно Аi либо относительно Еi путем введения третьей группы переменных – произвольных коэффициентов Us [1, 2, 3]
A1 = U1*E2 + U2*E3 A2 = - U1*E1 + U3*E3 (4) A3 = - U2*E1 – U3*E2
или
E1 = U1*A2 + U2*A3 E2 = — U1*A1 + U3*A3 (5) E3 = — U2*A1 – U3*A2
где U1, U2, U3 — произвольные коэффициенты, которые можно использовать для решения различных задач на многоообразии (3). Например, если хотим достигнуть максимум на поверхности F(x1, x2, x3) = 0 по переменной х3, то можем назначить произвольные коэффициенты U2 = -b*A1, U3 = - b*A2 и тогда получим
dx1/dt = U1*A2 – b*A1*A3 dx2/dt = — U1*A1 – b*A2*A3 (6) dx3/dt = b*(A1*A1 + A2*A2)
и если b > 0, тогда переменная х3 устойчиво стремится к максимуму, а для манипуляции траекторией остается коэффициент U1.
В общем случае, если имеем n переменных и m многообразий, ограничений, то число произвольных коэффициентов S будет равно числу сочетаний из n по m+1 [7], cм. таблицу 1,
m+1 S = C n > m (7) n
Число произвольных коэффициентов является мерой неопределенности и адаптивности. Лингво-комбинаторное моделирование может опираться на анализ всего корпуса текстов на естественном языке, это трудоемкая задача по извлечению смыслов для суперкомпьютеров, а также может использоваться, опираясь на ключевые слова в конкретной области, что позволяет получать новые модели для конкретных областей знания. В этом случае лингво-комбинаторное моделирование заключается в том, что в конкретной предметной области выделяются ключевые слова, которые объединяются во фразы типа (1), на основе которых строятся эквивалентные системы уравнений с произвольными коэффициентами. В частном случае они могут быть дифференциальными уравнениями и при их исследовании может быть использован хорошо разработанный математический аппарат. Лингво-комбинаторное моделирование включает все комбинации и все варианты решений и является полезным эвристическим приемом при изучении плохо формализованных систем [7, 8, 9]. В лингвистической литературе имеется множество трудов, в которых исследуются понятия смысла и значения, но эти теории во многом оказались неконструктивными, что ярко показал Л.Витгенштейн в своей Голубой книге. Использование в качестве модели фразы (1) уравнения (2) позволяет построить исчисление смыслов, которое хорошо реализуемо на компьютерах. По мнению Д.А.Леонтьева, смысл (будь то смысл текстов, фрагментов мира, образов сознания, душевных явлений или действий) определяется, во-первых, через более широкий контекст, и, во-вторых, через интенцию или энтелехию (целевую направленность, предназначение или направление движения). В нашем определении смысла наличествуют эти две характеристики – контекстуальность (смыслы вычисляются исходя из контекста) и интенциальность (произвольные коэффициенты позволяют задавать те или иные устремления).
Таблица 1
|
n / m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
2 |
1 |
|||||||
|
3 |
3 |
1 |
||||||
|
4 |
6 |
4 |
1 |
|||||
|
5 |
10 |
10 |
5 |
1 |
||||
|
6 |
15 |
20 |
15 |
6 |
1 |
|||
|
7 |
21 |
35 |
35 |
21 |
7 |
1 |
||
|
8 |
28 |
56 |
70 |
56 |
28 |
8 |
1 |
|
|
9 |
36 |
84 |
126 |
126 |
84 |
36 |
9 |
1 |
В философии существует большое направление – феноменология. Феноменология – это изучение сущностей [18,19]. Делят сущности на наблюдаемые и ненаблюдаемые. Можно трактовать лингво-комбинатороное моделирование как конструктивную феноменологию, как исчисление сущностей исходя из различных текстов на естественных и искусственных языках, при этом можно рассматривать как отдельные тексты, так и весь корпус текстов, накопленных человечеством. Каждый этносоциум обладает своим набором сущностей, который отличается от набора сущностей других энтосоциумов. Разнообразие этносоциумов – это богатство нашей планеты. В связи с глобализацией количество этносоциумов сокращается, что плохо.
2. Кибернетическая герменевтика
В древнегреческой мифологии посредником между богами и простыми смертными был Гермес, он должен был истолковывать людям повеления богов, а богам – просьбы людей. Отсюда и ведет свое происхождение термин «герменевтика», первоначально означающий искусство толкования изречений оракулов, древних текстов, знаков, смысла чужого языка и т.д. В средневековье герменевтика была неразрывно связана с теологией, с толкованием отцов церкви. Философская герменевтика возникла в середине Х1Х века, ее основоположником был Ф. Шлейермахер, который рассматривал герменевтику как метод всех наук о духе, доказывая, что с помощью психологического вживания можно проникнуть во внутренний мир авторов древних текстов, любых исторических деятелей и на этой основе реконструировать исторические события, понять их еще глубже, чем их осознавали сами участники этих событий. Х.-Г. Гадамер стремился отмежеваться от субъективизма своих предшественников, он провозглашает герменевтику универсальной философией нашего времени. По его убеждению именно «в языке выражается сам мир», становится видимой та действительность, которая «возвышается над сознанием каждого отдельного человека», ибо все, что является предметом познания и высказывания «всегда окружено мировым горизонтом языка». Для философа-структуралиста Мишеля Фуко язык – это самостоятельная «весомая и плотная реальность», в которую погружен человек и которая наряду с жизнью и трудом детерминирует его бытие. При этом язык трактуется широко и включает «немые привычки мысли», «тайный дух народов» у Фуко или «немотствующее удивление», «немую очарованность» у Гадамера. Гадамер рассматривает язык как опыт мира, язык как горизонт герменевтической онтологии, язык как среду герменевтического опыта, рассматривает формирование понятия «язык» в истории европейской мысли, язык и логос, язык и verbum, язык и образование понятий.
C появлением квантовой механики возникло мнение о том, что единого подхода в науке вообще быть не может. Это мнение отражено в высказывании одного из основоположников квантовой механики Нильса Бора о том, что описать процессы, протекающие в природе, с помощью одного языка невозможно. Необходимы разные описания, в каждом из которых яснее проявляются те или иные особенности изучаемого явления. То есть наука – это полилингвистическая система, где одновременно существуют и развиваются множества языков. С одной стороны это правильно, но с другой стороны существует универсальная знаковая система – естественный язык, который может быть единой основой описания единой природы, которую люди для простоты изучают в рамках отдельных специальностей. Но, как говорят, иная простота хуже воровства, сложившаяся фрагментарная картина мира уже не устраивает людей и наблюдается мощная тенденция интеграции наук и основой этой интеграции может быть структура естественного языка, который является мощной моделирующей системой. Предложенное лингво-комбинаторное моделирование может быть универсальным методом построения моделей с информационным управлением в самых различных отраслях науки.
Наличие возможности управления в текстах на естественном языке позволяет говорить о кибернетической герменевтике.
Язык смыслов Е может быть единым для всех естественных языков с учетом идиоматики. В свое время был предложен в качестве такого единого языка язык ЭСПЕРАНТО, но этот язык был придуман, это один из искусственных языков, которых развелось много в эпоху компьютеризации. Язык смыслов Е вычисляется из текстов на различных естественных языках, это прежде всего исчисление. В свое время Людвиг Витгенштейн мечтал об исчислении для языка в своей Голубой книге.
В качестве примера рассмотрим перевод с одного языка на другой язык. Если имеем фразу на одном языке и при переводе хотим сохранить смысл этой фразы из трех слов, то
phrase + word1 + word2 + word3
и после введения смыслов получим
(phrase)(sence0) + (word1)(sence1) + (word2)(sence2) + (word3) (sence3) = 0
или
А1*Е1 + А2*Е2 + А3*Е3 + А4*Е3 = 0
Разрешив это уравнение относительно Е, получим….
E1 = U1*A2 + U2*A3 + U3*A4 E2 = — U1*A1 + U4*A3 + U5*A4 E3 = — U2*A1 – U4*A2 + U6*A4 ( 10 ) E4 = — U3*A1 – U5*A2 – U6*A3
На другом языке, где A’ слова на другом языке, будем в частности иметь
E’1 = U1*A’2 + U2*A’3 + U3*A’4 E’2 = — U1*A’1 + U4*A’3 + U5*A’4 E’3 = — U2*A’1 – U4*A’2 + U6*A’4 (11) E’4 = — U3*A’1 – U5*A’2 – U6*A’3
Если мы хотим, чтобы смысл исходной фразы и переведенной сохранялся, то Е1 = Е’1, откуда вытекает
U1 (A2 — A’2) + U2(A3 – A’3) + U3(A4 – A’4) = 0 (12)
Использование этого уравнения определяет поиск слов на другом языке, соответствующих исходному языку в словарях.
3. Кибернетическая физика
Н.Винер, возродив кибернетику как управление и связь в живых организмах, машинах и социально-экономических системах, остановился как перед священной коровой перед физикой. Но за последние годы накопилось много нерешенных проблем, например, до сих пор не удалось установить связь с инопланетными цивилизациями, далее, стало очевидным, что видимая часть вселенной – это только 5%, а остальное – темная материя и темная энергия и нет единого мнения, что это за структуры, и список нерешенных проблем можно продолжить, что побуждает к поиску новых моделей.
Перейдем к построению лингво-комбинаторных моделей атомов, при этом будем исходить из ключевых базовых понятий, которые уже сложились в науке.
Рассмотрим в качестве примера атом водорода и в качестве ключевых слов возьмем слова «атом», «протон», «электрон», тогда фраза (1) будет иметь вид
Atom + Proton + Electron (13)
И в эквивалентных уравнениях (3), (4) и (5) А1 – характеристика атома водорода, Е1 – изменение этой характеристики, А2 – характеристика протона, Е2 – изменение этой характеристики, А3 – характеристика электрона, Е3 – изменение этой характеристики. Для моделирования дейтерия используем ключевые слова «атом», «протон», «электрон», «нейтрон»
Atom + proton + electron + neutron (14)
и эквивалентные уравнения будут
E1 = U1*A2 + U2*A3 + U3*A4 E2 = - U1*A1 + U4*A3 + U5*A4 E3 = - U2*A1 – U4*A2 + U6*A4 (15) E4 = - U3*A1 – U5*A2 – U6*A3
где U1, U2, U3, U4, U5, U6 – произвольные коэффициенты, А1 – характеристика атома дейтерия, Е1 – изменение этой характеристики, А2 – характеристика протона атома дейтерия, Е2 – изменение этой характеристики, А3- характеристика электрона атома дейтерия, Е3- изменение этой характеристики, А4 – характеристика нейтрона атома дейтерия, Е4 – изменение этой характеристики. В случае атомных реакций возможно превращение дейтерия в водород посредством трансформации уравнений (15) в уравнения (4).
Аналогичным образом возможно построение лингво-комбинаторных моделей всех известных элементов таблицы Менделеева и их изотопов и возможных новых элементов. Из структуры этих моделей вытекает наличие блока управления, который может манипулировать произвольными коэффициентами, то есть наша модель атома – это модель атома с блоком управления [8], разработка которой позволит осуществлять информационное воздействие на атомы. Это еще один путь для компьютерного моделирования физико-химических реакций. При этом необходимо решать задачу верификации таких моделей применительно к конкретным системам.
Структурная стабильность, совокупность устойчивых связей объекта, обеспечивающих его целостность и тождественность самому себе, т.е. сохранение основных свойств при различных внешних и внутренних воздействиях, обеспечивается адаптационными возможностями атомных и молекулярных систем [16 ]. В представленных лингво-комбинаторных моделях адаптационные возможности систем определяются числом произвольных коэффициентов в структуре эквивалентных уравнений и наибольшая структурная стабильность достигается в зоне адаптационного максимума, который обнаруживается у различных систем с числом переменных больше шести [ 7, 8 ], см таблицу. Для удержания систем в зоне адаптационного максимума можно использовать различные методы – рост числа переменных, наложение и снятие ограничений, объединение систем в коллективы. Действительно, если имеем две системы
m1+1 m2+1 S1 = C S2 = C (16) n1 n2
то путем наложения общих ограничений mcol получим коллектив
m1+m2+mcol +1 Scol = C (17) n1+n2
При этом в зависимости от конкретных параметров может быть Scol > S1 + S2, когда объединение в коллектив приводит к росту адаптационных возможностей, а может быть Scol < S1 + S2, когда адаптационные возможности меньше суммы адаптационных возможностей исходных систем. Лингво-комбинаторное моделирование может явиться полезным инструментом при анализе и синтезе атомно-молекулярных систем.
Представляется интересным рассмотреть вопрос о путях перехода из одной мировой точки в другую.Обычное трехмерное пространство и время образуют четырехмерный мир. Мировая точка есть обычная точка в некоторый момент времени. Ее четырьмя координатами являются декартовы координаты X,Y,Z и время t, которые будем обозначать через х1, х2, х3, х4. Событие есть физическое явление в некоторой мировой точке. Четырехмерное расстояние х9 между двумя мировыми точками х1, х2, х3, х4 и х5, х6, х7, х8, интервал, определяется как
с 2 (х4 – х8) 2 – (х1 – х5) 2 – (х2 – х6) 2 – (х3 – х7) 2 = (х9) 2
где с – скорость света, (х4 – х8) – дельта Т, разница во времени.
Возможные различные пути перехода из одной мировой точки в другую и представляет большой интерес исследование всего множества этих путей перехода. К сожалению в многочисленных работах по теории относительности этот вопрос не исследован, что определило тупик в изучении свойств пространства и времени. Методика лингво-комбинаторного моделирования может быть использована для изучения и этой проблемы.
После дифференцирования вышеуказанного уравнения можно построить систему эквивалентных уравнений с произвольными коэффициентами, число которых в данном случае будет 36, которые и могут быть использованы для задания различных движений. Можно задать сближение мировых точек по различным законам, в том числе и по законам Ньютона, и исследовать, как влияет тяготение и другие силы на время и пространство и на поведение нанороботов. Возможно перемещение нанороботов в настоящее время из прошлого или будущего. Сходство нанороботов с вирусами позволяет предполагать, что и вирусы могут проникать в наше настоящее как из прошлого, так и из будущего, что представляется важным для здравоохранения.
В настоящее время поставлена задача создания нанороботов, которые могли бы манипулировать атомно-молекулярными структурами как строя из этих структур наносооружения, так и разбирая наносооружения по мере надобности. Уже имеется большой опыт создания человекоразмерных робототехнических систем, отработаны их алгоритмы функционирования при манипулировании различными предметами, при сборке и разборке различных машин и сооружений [1,2]. Переход на наноразмеры оказывается непростым делом. Химия представляет очень большой спектр веществ, из которых могли бы синтезироваться нанороботы, и для сокращения этого списка и выбора подходящих веществ как раз и нужно выработать необходимые и достаточные условия синтеза нанороботов. Для решения этой задачи прежде всего необходим единый язык описания как атомно-молекулярных структур, так и алгоритмов функционирования будущих нанороботов. Такой общий язык описания предлагается методом лингво-комбинаторного моделирования [4, 5, 7, 8]. Наноструктуры должны понимать естественный язык. Сегодня имеется множество барьеров между человеком и наноструктурами. Лингво-комбинаторное моделирование поможет преодолеть эти барьеры в физике, химии, биологии и других науках.
В наноструктурах одна из главных проблем – это проблема сборки. Наноробот должен взять атом и перенести его в другое место, по сути дела перевести его из одной мировой точки в другую. В качестве исходного рассмотрения можно взять механическую трехзвенную руку манипулятора, который может переносить предметы из одной точки в другую, где Х1, Х2, Х3 и Х4, Х5, Х6 – координаты концов первого жесткого звена длиной L1, Х4, Х5, Х6 и Х7, Х8, Х9 – координаты концов второго жесткого звена длиной L2, Х7, Х8, Х9 и Х10, Х11, Х12 – координаты концов третьего жесткого звена длиной L3, тогда исходные уравнения трехзвенной руки манипулятора будут
2 2 2 2
(X1 – X2) + (X2 – X5) + (X3 – X6) = L1
2 2 2 2
(X4- X7) + (X5 – X8) + (X6 – X9) = L2
2 2 2 2
(X7 – X10) + (X8 – X11) + (X9 – X12) = L3
и эквивалентные уравнения будут содержать
m+1 4 S = C = C = 792 n 12
произвольных коэффициента. Некоторые молекулы имеют примерно такое же количество произвольных коэффициентов, именно среди них и необходимо искать те вещества, из которых можно синтезировать наноробота, который мог бы переносить атом из одного места в другое.
Таков аналитический путь выбора веществ для синтеза нанороботов.
В качестве итогов нашего рассмотрения можно сформулировать необходимые условия для синтеза наноробота – сложность веществ, из которых синтезируется наноробот должна быть больше сложности реализуемых нанороботом алгоритмов.
В качестве достаточного условия существования наноробота в изменяющейся среде необходимо, чтобы наноробот находился в зоне адаптационного максимума. Тогда он сможет в полной мере использовать свои возможности и обеспечить свою выживаемость в максимально возможной зоне изменений окружающей среды. Наличие произвольных коэффициентов и возможность расширения модели, возможность включения новых переменных, новых ключевых слов, позволяют настраивать модель для моделирования сложных наноструктур.
4. Кибернетическая астрономия и астрофизика
Человечество издревле наблюдало и изучало космос, который безусловно влиял на развитие человечества. В процессе своего развития человечество создавало самые различные артефакты – здания, дороги, машины и т.д., но самым значительным артефактом, созданным человечеством, является естественный язык, который вобрал и вбирает все знания, навыки, учения, созданные людьми на сознательном и подсознательном уровне. Поэтому очевидно стремление обратиться к естественному языку для того, чтобы глубже понять, как устроена вселенная [7,19].
Если обратиться к моделированию солнечной системы, то в качестве ключевых слов можно взять Солнце, Меркурий, Венеру, Землю, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон – 10 переменных, в структуре эквивалентных уравнений этой системы будет содержаться 45 произвольных коэффициентов
E1=U1*A2+U2*A3+U3*A4+U4*A5+U5*A6+U6*A7+
U7*A8+U8*A9+U9*A10
E2=-U1*A1+U10*A3+U11*A4+U12*A5+U13*A6+U14*
A7+U15*A8+U16*A9+U17*A10
E3=-U2*A1-U10*A2+U18*A4+U19*A5+U20*A6+U21*A7+U22*
A8+U23*A9+U24*A10
E4=-U3*A1-U11*A2-U18*A3+U25*A5+U26*A6+U27*A7*+U28*
A8+U29*A9+U30*A10
E5=-U4*A1-U12*A2-U19*A3-U25*A4+U31*A6+U32*A7+U33*A8
+U34*A9+U35*A10
E6=-U5*A1-U13*A2-U20*A3-U26*A4-U31*A5+U36*A7+U37*A8
+U38*A9+U39*A10
E7=-U6*A1-U14*A2-U21*A3-U27*A4-U32*A5-U36*A6+U40*A8
+U41*A9+U42*A10
E8=-U7*A1-U15*A2-U22*A3-U28*A4-U33*A5-U37*A6-U40*A7+
U43*A9+U44*A10
E9=-U8*A1-U16*A2-U23*A3-U29*A4-U34*A5-U38*A6-U41*
A7-U43*A8+U45*A10
E10=-U9*A1-U17*A2-U24*A3-U30*A4-U35*A5-U39*A6-U42*
A7-U44*A8-U45*A9
В этой системе уравнений А1-характеристика Солнца, Е1- изменение этой характеристики, А2-характеристика Меркурия, Е2-изменение этой характеристики,…, U1,U2…U45 – произвольные коэффициенты, наличие которых определяет возможность управления характеристиками. Выявление этой новой возможности управления важна для человечества ввиду астероидной опасности. Наша планета хранит свидетельства разрушительного воздействия астероидов, падение которых вызывало глобальные катастрофы. В настоящее время налаживается мониторинг околоземного пространства и выявляются все новые и новые аспекты астероидной опасности. Для борьбы с астероидной опасностью планируется использовать всю мощь накопленного ядерного оружия землян, но в случае если размеры астероида будут превышать 10 километров в диаметре, то и это средство не поможет. Единственная надежда – на открытие новых способов управления планетарными процессами. Аналогичным образом возможно моделирование галактик и их взаимодействия. Обратимся к анализу предложенной модели.
Во-первых, когда мы говорим о системе, это значит, что из всего мы выделяем часть – систему и рассматриваем ее взаимодействие с оставшимся, с окружающей средой. Также и с солнечной системой – мы выделили планеты и можем рассматривать как взаимодействие между ними, так и воздействие остального космоса на всю солнечную систему. Солнечная система существует в потоке переменных воздействий остального космоса и ее устойчивость зависит от ее адаптационных возможностей, которые определяются числом произвольных коэффициентов. В данном случае это число 45, в общем случае оно определяется формулой (7). Как очевидно из этой формулы, в зависимости от числа наложенных ограничений для числа переменных больше шести количество произвольных коэффициентов будет сначала возрастать, достигнет максимума и потом будет уменьшаться. Это явление в теории систем называется феноменом адаптационного максимума [1,2,3], в зоне адаптационного максимума система обладает максимальными адаптационными возможностями. Можно предположить, что в процессе эволюции адаптационные возможности солнечной системы изменяются в соответствии с формулой (7), что можно подтвердить или опровергнуть соответствующими исследованиями. Формула (7) может быть основой для объяснения ритмов развития как солнечной системы в целом, так и солнца в частности, и галактических систем.
Во-вторых, в качестве ключевых слов для построения модели мы взяли сами планеты, которые можно наблюдать, то есть это феноменологическая модель. Люди издревле наблюдали планеты и для объяснения их движения создали целую систему понятий, в частности для объяснения их движения были привлечены законы Ньютона, которые опираются на понятия «сила», «масса», «ускорение», «скорость». Опираясь на эти понятия как на ключевые слова можно нашим методом построить другую лингво-комбинаторную модель, которая бы определила взаимодействие между этими понятиями. Таким образом можно рассматривать два языка – язык феноменологического описания и язык научных теорий и попытаться осуществить перевод с одного языка на другой язык, а можно замешать в общую структуру как сами явления, так и научные понятия, что и определит взаимодействие между ними.
В-третьих, о прямых и обратных задачах. Прямая задача связана с моделированием следствия по заданной причине. В обратной задаче мы хотим восстановить причину по известному следствию. Прямая задача имеет единственное и устойчивое к малым возмущениям решение. Для обратной задачи единственность решения может нарушаться, т.к. различные причины могут вызвать одно и тоже следствие. Если обратиться к движению планет, которое наблюдается людьми много тысяч лет, то этот феномен может быть по-разному объяснен. Существовала система Птолемея, потом были открыты законы Кеплера, потом законы Ньютона. Если считать за причину законы Ньютона, то исходя из них можно рассчитать траектории движения планет. Но исходя из других соображений тоже можно получить такое же движение планет, такой же феномен. Эта обратная задача, которая имеет множество решений [19]. Лингво-комбинатороное моделирование позволяет построить множество различных генераторов таких же движений.
В-четвертых, в современной науке и в обществе в настоящее время получили большое распространение понятия «управление», «информация» и они пронизывают биологические науки ( от генетики до высшей нервной деятельности), социально-экономические науки, технические науки, но эти понятия можно сказать исключены из физики и астрономии в частности. Конечно, и астрономия , и физика сформировались довольно давно, когда понятия «управление» и «информация» не были разработаны, но в настоящее время вызывает недоумение отсутствие этих понятий при объяснении многих астрономических и физических явлений. Если исходить из этой точки зрения, то насущной задачей астрофизики должен быть поиск центров управления, систем связи и самой возможности управления малыми воздействиями, вызывающими большие последствия в планетарных и галактических системах. В 1949г Норберт Винер возродил кибернетику, опубликовав книгу «Управление и связь в животном и машине» , но он не стал распространять принципы кибернетики на физику, остановился перед ней как перед священной коровой. В настоящее время рассматривается вопрос о создании кибернетической физики, в которой вопросы управления займут достойное место.
Уже существует гипотеза Гея, в которой рассматривается вся планета Земля как живая система. Можно высказать гипотезу о живой вселенной со своей нервной системой.
В-пятых, еще в Древней Греции Анаксимандром была высказана гипотеза о существовании апейрона – субстанции, которая пронизывает вся и все. В свете развиваемой нами теории апейрон – физическая символьная структура, которая реализует структурированную неопределенность в виде произвольных коэффициентов U, субстанции U. Структурированной неопределенности противопостоит хаос – неструктурированная неопределенность. Структурированная неопределенность – основа жизни во вселенной. В свете развиваемой теории, вакуум – это непрерывно перестраиваемая матрица структурированной неопределенности, в которой заполнение матрицы идентифицируется с назначением конкретных значений произвольным коэффициентам U. Перед астрономами и астрофизиками стоит задача обнаружения центров управления планетарными и галактическими системами. Эти идеи перекликаются с идеями К.Э.Циолковского, стопятидесятилетие со дня рождения мы будем отмечать в 2007г.
5. Кибернетическая экономика
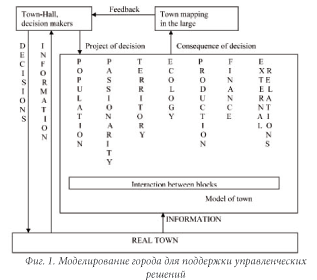
В качестве другого примера рассмотрим проблему моделирования города.
Если в качестве ключевых слов взять «население», «пассионарность», «территория», «производство», «экология и безопасность», «финансы», «внешние связи», то в соответствии с вышеизложенной методикой уравнение города будет
А1*Е1 + А2*Е2 + …+А7*Е7 = 0 (18)
а эквивалентные уравнения будут иметь вид
E1 = U1*A2 + U2*A3 + U3*A4 + U4*A5 + U5*A6 + U6*A7
E2 = - U1*A1 + U7*A3 + U8*A4 + U9*A5 + U10*A6 + U11*A7
E3 = - U2*A1 – U7*A2 + U12*A4 + U13*A5 + U14*A6 + U15*A7
E4 = - U3*A1 – U8*A2 – U12*A3 + U16*A5 + U17*A6 + U18*A7 (19)
E5 = - U4*A1 – U9*A2 – U13*A3 – U16*A4 + U19*A6 + U20*A7
E6 = - U5*A1 – U10*A2 – U14*A3 – U17*A4 – U19*A5 + U21*A7
E7 = - U6*A1 – U11*A2 – U15*A3 – U18*A4 – U20*A5 – U21*A6
где А1 – характеристика населения, которая включает в себя характеристики здоровья, образования, занятости; Е1 – изменение этой характеристики; А2 – характеристика пассионарности, устремлений групп населения, люди обладают свободой выбора при принятии решений и этот выбор является важным, что оценивается путем социологического анализа; Е2 – изменение этой характеристики; А3 – характеристика территории, включая наземные и подземные постройки, этот блок может быть геоинформационной системой; Е3 – изменение этой характеристики; А4 – характеристика производства, включая оценку различных видов деятельности – научной, производственной, транспортной, торговой и др.; Е4 – изменение этой характеристики; А5 – характеристика экологии и безопасности; Е5 – изменение этой характеристики; А6 – характеристика финансов, финансовых потоков и запасов в городе; Е6 – изменение этой характеристики; А7 – характеристика внешних связей города, включая оценку входящих и выходящих потоков людей, энергии, материалов, информации, финансов; Е7 – изменение этой характеристики; U1, U2,…,U21 – произвольные коэффициенты, которые могут быть использованы для управления и решения различных задач на многообразии (13).
Эта модель (Фиг. 1) используется в системах для поддержки принятия решений городскими властями [14].
Любой этносоциум может описываться аналогичной моделью.
6. Кибернетическая биология
ДНК и человеческая речь обладают стратегически близкой фрактальной структурой, существует родство фракталов ДНК и человеческой речи
В качестве примера рассмотрим модель ментальных процессов. Обычно ментальные процессы характеризуются ключевыми словами «восприятие», «внимание», «память», «мышление», «язык», «эмоции», «управление движениями» и тогда структура эквивалентных уравнений будет иметь вид (14), где А1 – характеристика восприятия, Е1 – изменение этой характеристики, А2 – характеристика внимания, Е2 – изменение этой характеристики, А3 – характеристика памяти, Е3 – изменение этой характеристики, А4 – характеристика мышления, Е4 – изменение этой характеристики, А5 – характеристика языка, Е5 – изменение этой характеристики, А6 – характеристика эмоций, Е6 – изменение этой характеристики, А7 – характеристика управления движениями, Е7 – изменение этой характеристики. Уравнения (19) определяют взаимодействие между различными составляющими ментальных процессов в рамках нашей модели. Из этой модели вытекает необходимость в блоке управления для манипуляции произвольными коэффициентами. Этот блок управления можно считать аналогом высшей психической структуры – личности.
Для построения другой модели ментальных процессов можно исходить из структуры естественного языка, и если он содержит сто тысяч различных слов, то мозг человека в соответствии с формулой (7) будет содержать такое количество произвольных коэффициентов, порядок которого совпадает с количеством нейронов мозга (lgS = 10, Л.1). Можно высказать предположение, что нейроны в мозгу – это и есть субстанция произвольных коэффициентов, субстанция U, которая пронизывает все и вся и наличие которой в принципе позволяет управлять атомными и молекулярными процессами с помощью ментальных процессов. Развитие естественного языка приводит к развитию субстанции U, к усилению человеческих возможностей по управлению. Ментальные процессы являются частью целостного организма.
В качестве следующего примера рассмотрим моделирование организма. Организм человека – очень сложная система, которую можно рассматривать на уровне молекул, клеток, органов. Для лечащего врача важно рассмотрение организма прежде всего на уровне органов и при построении лингво-комбинаторной модели мы будем исходить из общепринятого набора органов — «органы движения», «органы пищеварения», «органы дыхания», «мочеполовые органы», «кроветворная и лимфатическая системы», «центральная нервная система», «периферийная нервная система», «железы внутренней секреции», «кожа и сенсорные системы», уравнение организма будет содержать девять переменных
A1*E1 + A2*E2 + . . .+ A9*E9 = 0 (20)
а структура эквивалентных уравнений будет иметь вид (21)
Е1 = U1*A2 + U2*A3 + U3*A4 + U4*A5 + U5*A6 + U6*A7 + U7*
A8 + U8*A9
E2 = -U1*A1+U9*A3+U10*A4+U11*A5+ +U12*A6+U13*A7+
U14*A8+U15*A9
E3 = - U2*A1-U9*A2+U16*A4+U17*A5+ +U18*A6 +U19*A7+
U20*A8+U21*A9
E4 = - U3*A1-U10*A2-U16*A3+U22*A5+U23*A6+U24*A7+
U25*A8+U26*A9
E5 = - U4*A1-U11*A2-U17*A3-U22*A4 +U27*A6+U28*A7+
U29*A8+U30*A9
E6 = - U5*A1-U12*A2-U18*A3-U23*A4-U27*A5+U31*A7+U32*
A8+U33*A9
E7 = - U6*A1-U13*A2-U19*A3-U24*A4-U28*A5-U31*A6+U34*
A8+U35*A9
E8 = — U7*A1-U14*A2-U20*A3-U25*A4-U29*A5-U32*A6-U34*
A7+U36*A9
E9 = — U8*A1-U15*A2-U21*A3-U26*A4-U30*A5-U33*A6-U35*
A7-U36*A8
где U1, U2, . . . ,U36 – произвольные коэффициенты, которые могут быть использованы для настройки модели; А1 – характеристика органов движения, Е1 – изменение этой характеристики, и т.д. Эта модель используется в страховой медицине [23].
Изложенная выше модель базируется на западном представлении об организме, но существуют и другие представления о такой сложной системе как организм. Существовала и развивается восточная медицина с очень своеобразным делением организма на подсистемы, при этом в Индии используется одно представление об организме, а в Китае – другое. Наряду с официальной медициной существует так называемая народная медицина. Наши знания об организме содержат очень большую неопределенность, что и позволяет сосуществовать различным представлениям об организме и различным методам лечения. В свое время Э. Шредингер написал книгу «Что такое жизнь? С тоски зрения физики», в наши дни необходимо написать книгу «Что такое жизнь с точки зрения кибернетики и информатики»
7. Кибернетическая метеорология
Если обратиться к моделированию атмосферы, то в качестве ключевых слов можно взять метеорологические элементы – «температура», «давление воздуха», «влажность воздуха», «скорость ветра», «направление ветра», «облачность», «осадки», «видимость (прозрачность атмосферы)», «температура почвы», «температура поверхности воды» – 10 переменных, в структуре эквивалентных уравнений этой системы будет содержаться 45 произвольных коэффициентов
E1=U1*A2+U2*A3+U3*A4+U4*A5+U5*A6+U6*A7+
U7*A8+U8*A9+U9*A10
E2=-U1*A1+U10*A3+U11*A4+U12*A5+U13*A6+U14*
A7+U15*A8+U16*A9+U17*A10
E3=-U2*A1-U10*A2+U18*A4+U19*A5+U20*A6+U21*A7+U22*
A8+U23*A9+U24*A10
E4=-U3*A1-U11*A2-U18*A3+U25*A5+U26*A6+U27*A7*+U28*
A8+U29*A9+U30*A10
E5=-U4*A1-U12*A2-U19*A3-U25*A4+U31*A6+U32*A7+U33*
A8+U34*A9+U35*A10
E6=-U5*A1-U13*A2-U20*A3-U26*A4-U31*A5+U36*A7+U37*
A8+U38*A9+U39*A10
E7=-U6*A1-U14*A2-U21*A3-U27*A4-U32*A5-U36*A6+U40*
A8+U41*A9+U42*A10
E8=-U7*A1-U15*A2-U22*A3-U28*A4-U33*A5-U37*A6-U40*A7+
U43*A9+U44*A10
E9=-U8*A1-U16*A2-U23*A3-U29*A4-U34*A5-U38*A6-U41*
A7-U43*A8+U45*A10
E10=-U9*A1-U17*A2-U24*A3-U30*A4-U35*A5-U39*A6-U42*
A7-U44*A8-U45*A9
В этой системе уравнений, которая у нас будет иметь номер 22, А1-характеристика температуры воздуха, Е1- изменение этой характеристики, А2-характеристика давления, Е2-изменение этой характеристики,…, U1,U2…U45 – произвольные коэффициенты, наличие которых определяет возможность управления характеристиками. Выявление возможности управления важна для подстройки модели и для управления погодой. Предсказанием погоды люди занимались испокон веков и при этом базировались на самых различных представлениях о природных явлениях и их взаимодействии, но атмосфера – очень сложная система и все ее описания содержат большую неопределенность что и объясняет неточность прогнозов.
8. Адаптационные возможности сложных систем
В структуре эквивалентных уравнений систем со структурированной неопределенностью есть произвольные коэффициенты, которые можно использовать для приспособления системы к различным изменениям чтобы повысить точность и надежность функционирования систем, их живучесть в потоке перемен.
5.3. Феномен адаптационного максимума в жизненном цикле сложных развивающихся систем
Социально-экономические системы – семья, предприятия, банки, города, села, регионы, страны проходят сложный путь развития, находясь под воздействием различных внутренних и внешних факторов. Одни предприятия и банки процветают, другие терпят крах и банкротятся, одни города и страны процветают, другие переживают стагнацию, о чем свидетельствует мировая статистика. Все эти социально-экономические системы являются сложными развивающимися системами и в жизненном цикле этих систем проявляются закономерности, свойственные многомерным системам.
Важной закономерностью, оказывающей большое влияние на социально-экономические системы, является феномен наличия адаптационного максимума, который заключается в следующем[7,8,9 ].
Установлена ранее неизвестная закономерность наличия адаптационного максимума в жизненном цикле сложных развивающихся систем, заключающаяся в том, что при наложении ограничений на систему из n переменных ( n > 6) число произвольных коэффициентов в структуре эквивалентных уравнений, описывающих поведение системы, сначала возрастает, достигает максимума, а потом начинает убывать, и соответственно изменяются адаптационные возможности системы – сначала они растут, достигают максимума, а потом начинают убывать, и если наложение ограничений продолжается, то система делается жесткой и погибает в потоке перемен окружающей среды, откуда вытекает стратегия управления различными сложными системами – они должны управляться так, чтобы удержать их в зоне адаптационного максимума, если хотим обеспечить их живучесть в потоке перемен.
Таблица 2
|
Years/age |
1896-1897 |
1958-1959 |
1969-1970 |
1978-1980 |
1982-1983 |
1984-1985 |
|
0 – 4 |
133,0 |
11,9 |
6,9 |
8,1 |
7,9 |
7,7 |
|
5 – 9 |
12,9 |
1,1 |
0,7 |
0,7 |
0,6 |
0,6 |
|
10 – 14 |
5,4 |
0,8 |
0,6 |
0,5 |
0,5 |
0,5 |
|
15 – 19 |
5,8 |
1,3 |
1,0 |
1,0 |
1,0 |
0,9 |
|
20 – 24 |
7,6 |
1,8 |
1,6 |
1,7 |
1,6 |
1,5 |
|
25 – 29 |
8,2 |
2,2 |
2,2 |
2,3 |
2,2 |
2,0 |
|
30 – 34 |
8,7 |
2,6 |
2,8 |
2,9 |
2,9 |
2,8 |
|
35 – 39 |
10,3 |
3,1 |
3,7 |
4,3 |
3,8 |
3,6 |
|
40 – 44 |
11,8 |
4,0 |
4,7 |
5,4 |
5,6 |
5,7 |
|
45 – 49 |
15,7 |
5,4 |
6,0 |
7,8 |
7,4 |
7,3 |
|
50 – 54 |
18,5 |
7,9 |
8,7 |
10,3 |
10,9 |
11,3 |
Уже давно известно, что существуют ритмы в биологических системах. Например, из результатов переписи населения (таблица 2) ясно видно наличие минимума смертности для людей в возрасте 10-14 лет, при этом следует отметить, что он сохраняется независимо от социально – экономических условий – и в период 1896-1897 годов, и в период 1984-1985 годов, но объяснения этому минимуму смертности не было. Из статистики развития экономики известны циклы Кондратьева и другие циклические явления в экономике как отдельных предприятий, так и более крупных экономических образований. В технических системах известны периоды максимальной надежности и устойчивости систем. Предложенная математическая модель развивающихся систем позволяет говорить о наличии закономерности адаптационного максимума, которая объясняет многочисленные факты и позволяет предсказывать поведение сложных систем.
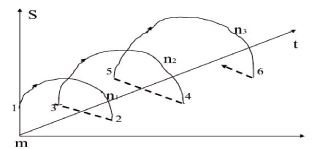
Фиг. 6. Трансформация развивающейхся системы, n1<n2<n3,траектория системы : 1-2-3-4-5-6-…
Система – целостная совокупность элементов, в которой все элементы настолько тесно связаны между собой, что она выступает по отношению к другим системам и окружающей среде как нечто единое. На Fig.3 представлена схема, где система взаимодействует со средой и использует два механизма адаптации – а — настойка или самонастройка системы с помощью произвольных коэффициентов в структуре эквивалентных уравнений системы, — б- обучение или самообучение системы, которая заключается в наложении новых ограничений на систему. Кроме этих механизмов адаптации возможны и другие, такие как рост числа переменных системы, размножение, эффективное забывание, ограничение контактов со средой, объединение систем в коллектив и др. В общем случае число произвольных коэффициентов S в структуре эквивалентных уравнений системы определяется как число сочетаний из n по m+1 и определяется формулой (7) (см. Таблицу 1)
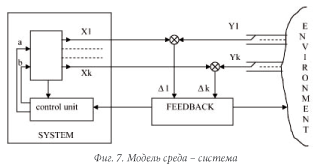
Сложная система – это система, в которой проявляется феномен адаптационного максимума, то есть система с числом переменных больше шести. На Фиг. 7 представлена схема взаимодействия вышеописанной системы с окружающей средой, где переменные системы х1,…,хк взаимодействуют с переменными среды у1,…,ук, а сигналы рассогласования передаются в блок
управления, и у системы есть две возможности приспособиться к изменениям в среде, это, во-первых, настойка с помощью манипуляции произвольными коэффициентами, и чем больше этих коэффициентов, тем выше адаптационные возможности, и, во-вторых, обучение, наложение новых ограничений на переменные системы. В режиме непрерывного обучения число произвольных коэффициентов изменяется в соответствии с формулой (7), и это приводит к появлению циклов в развитии систем, что иллюстрируется на Fig.2, где цикл развития системы начинается в точке 1, проходит через максимум в числе произвольных коэффициентов и заканчивается в точке 2, где должна наступить трансформация, сброс ранее накопленных ограничений, далее начинается в точке 3 новый цикл, опять система проходит через максимум адаптационных возможностей, достигает точки 4, где опять происходит трансформация, и система начинает новый цикл в точке 5 и так далее. Эта модель позволяет объяснить наличие циклов в развитии сложных биологических, социально-экономических и технических систем.
Предложенная модель процессов самоорганизации сложных развивающихся систем реализует закономерность наличия адаптационного максимума в жизненном цикле систем в потоке перемен. Жизненный цикл – совокупность фаз развития, пройдя через которые система достигает зрелости и становится способной эффективно функционировать и дать начало новому поколению.
Как показывает статистика, существуют циклы в развитии экономики, в частности — циклы Кондратьева. Учет закономерности наличия адаптационного максимума позволяет объяснить эти циклы [32]. Надежность сложных человеко-машинных комплексов достигает своего максимума в зоне адаптационного максимума и технические системы должны строиться таким образом, чтобы при изменении этих систем они оставались в зоне адаптационного максима как можно дольше.
Число примеров систем можно было бы увеличивать, но уже ясно, что феномен адаптационного максимума существует и учет закономерности наличия адаптационного максимума в жизненном цикле сложных развивающихся систем позволит лучше понять механизмы их функционирования и значительно улучшить их характеристики. Для того, чтобы выжить, этносоциум должен находиться в зоне адаптационного максимума.
Наличие феномена адаптационного максимума в жизненном цикле различных сложных развивающихся систем позволяет объяснить эволюцию систем в условиях изменяющейся среды. Феномен адаптационного максимума является основой самоорганизации в природе и обществе. Структура неопределенных коэффициентов задает матрицу картины мира, в рамках которой и разыгрываются различные события.
Лингво-комбинаторное моделирование – это универсальный метод моделирования плохо формализованных систем в самых различных областях науки, техники, в различных областях человеческой деятельности. В каждом конкретном применении этого метода необходимо осуществлять верификацию модели, проверять ее на соответствие поведению реального объекта. Наличие произвольных коэффициентов и возможность расширения модели, возможность включения новых переменных, новых ключевых слов, позволяют настраивать модель для моделирования сложных реальных объектов.
Заключение
Лингво-комбинаторное моделирование позволяет сформировать новую картину мира, которая опирается на все достижения современной науки и прежде всего информатики. Лингво-комбинаторная картина мира состоит из трех групп переменных, во-первых, это явления (Appearances), во-вторых, это смыслы (Essences), в-третьих – это структурированная неопределенность (Structural Uncertainty), из которых состоят все неживые и живые системы. Лингво-комбинаторное моделирование – это математический аппарат постнеклассической науки. На уровне неклассической науки был введен наблюдатель, на уровне постнеклассической науки введен управитель[31].
Время разделения наук по отдельным специальностям заканчивается, наступает время интеграции и для этого есть прекрасный инструмент – вычислительные системы. Разделение наук на фундаментальные и прикладные условно. Но развитие кибернетики и информатики безусловно внесло и будет вносить новое в наше представление о мире в целом, а это и есть фундаментальная наука.
Литература
1. Максвелл Д.К., Вышнеградский И.А., Стодола А. « Теория автоматического регулирования» М., 1949.
2. «Автоматизация производства и промышленная электроника» Энциклопедия современной техники под ред. А.И.Берга и В.А.Трапезникова, тома 1-4, М., 1962-1965.
3.«Энциклопедия кибернетики» под ред. В.М.Глушкова, Киев, 1974
4.Баранова И.В., Баранов Д.М. «Русский язык. Периодическая система элементов русской речи» Санкт-Петербург, 2000.
5. «Computational Science: Ensuring America’s Competitiveness» President’s Information Technology Advisory Committee. May 27, 2005.
6. Игнатьев M.Б. «Голономные автоматические системы» М — Л, изд. АН СССР, 1963.
7. Ignatiev M. B. ”Simulation of Adaptational Maximim Phenomenon in Developing Systems” Proceedings of The SIMTEC’93 — 1993 International Simulation Technology Conference, San Francisco, USA, 1993, p.41-42.
8. Ignatyev M.B.,D.M.Makina, N.N.Petrischev, I.V.Poliakov, E.V.Ulrich, A.V.Gubin “Global model of organism for decision making support” Proceedings of the High Performance Computing Symposium – HPC 2000, Ed. A. Tentner, 2000 Advanced Simulation Technologies Conference, Washington D.C. USA, 2000, p.66-71.
9. Ignatyev M. B. “Linguo-combinatorial method for complex systems simulation” Proceedings of the 6 th World Multiconference on Systemics, Cybernetics and Informatics, vol. XI, Computer science II, Orlando, USA, 2002, p.224-227.
10. Ignatyev M. B., Pinigin G. I. “Linguo-combinatorial simulation of universe” XXV General Assembly of International Astronomical Union, Sydney, Australia, 2003 www.astronomy2003.com
11. Бейдер Р. «Атомы в молекулах» М, изд. Мир, 2001.
12. Игнатьев М.Б. «Самоорганизующиеся робототехнические системы и игра в футбол» Сборник трудов Первой международной конференции по механотронике и робототехнике», том 2, стр. 127-131, Санкт-Петербург, 2000.
13. Кара-Мурза С.Г. «Манипуляция сознанием» М, 2000.
14. .М.Б.Игнатьев «Рекурсивные вычислительные машины» журнал «Информационно-управляющие системы» №5, 2004, стр.54-57
15. А.Е.Войскунский, М.Б.Игнатьев, А.В.Никитин, М.А.Селисская «Применение виртуальной реальности в качестве психотерапевтического средства для помощи страдающим от психологических фобий» Труды У11 всероссийской объединенной конференции «Интернет-технологии и современное информационное общество», 2004, С-Петербург, стр.10-12.
16. А.Ю.Замятин, М.Б.Игнатьев «Проблемы информатизации регионов России на основе многослойного Интернета» Тезисы докладов Ш международной конференции «Интернет нового поколения iPv6», 2004, Москва,стр.33-38.
17. М.Б.Игнатьев «Роботы, аватары и люди как системы со структурированной неопределенностью» Материалы Всероссийской междисциплинарной конференции «Философия искусственного интеллекта»2005, Москва, стр.1005-110.
18. М.Б.Игнатьев, А.В.Никитин, А.А.Никитин, Б.Н.Миронов «Кибернетический велосипед в системах образования, оздоровления и развлечения» Информатизация сельской школы, Труды П всероссийского научно-методического симпозиума, Анапа-Москва, 2004, стр.103-108.
19. М.Б.Игнатьев, Ю.Е.Шейнин «Рекурсивные вычислительные системы» журнал «Информатизация и связь» №2, 2005, стр.33-40.
20. С.И.Богданов, М.Б.Игнатьев, А.В.Никитин «Образовательные виртуальные миры Петербурга» журнал «Информатизация и связь» №2, 2005, стр.28-32.
21. М.Б.Игнатьев, А.А.Никитин, А.В.Никитин, Н.Н.Решетникова «Архитектура виртуальных миров» монография, С-Петербург, 2005.
22. М.Б.Игнатьев «Закономерность изменения адаптационных возможностей в жизненном цикле сложных развивающихся систем» Диплом № 25-S на открытие в области кибернетики и системного анализа с приоритетом от 28.06.1963.
23. М.Б.Игнатьев, А.В.Никитин, А.А.Оводенко «Панорама Второй мировой войны и битвы за Ленинград на основе технологии виртуальных миров» Труды УШ всероссийской конференции «Технологии информационного общества – Интернет и современное общество» 2005, С-Петербург, стр.69-71.
24. М.Б.Игнатьев, А.В.Никитин, Н.Н.Решетникова «Технология виртуальных миров как основа ИТ-образования» Сб.трудов «Современные информационные технологии и ИТ-образование» 2005, Москва, стр.103-110.
25. М.Б.Игнатьев «Информатизация и новая картина мира» журнал «Информатизация и связь» №4, 2005, стр.3-10.
26. M.Ignatyev “The study of the Adaptation Phenomenon in Complex System” AIP Conference Proceedings, Melville, New York, 2006, vol. 839, p.322-330.
27. М.Б.Игнатьев «Лингво-комбинаторное моделирование для решения плохо формализованных задач» Тезисы докладов Второй международной конференции по когнитивной науке, 2006, С-Петербург, стр.285.
28. М.Б.Игнатьев «Робот стал элементом культуры» газета Известия от 11.08.2006
29. В.И.Дмитриев «О методах решения обратных задач» Вестник МГУ, серия 15 «Вычислительная математика и кибернетика» №4, 2001, стр.3-7.
30. Д.А.Леонтьев «Психология смысла – природа, строение и динамика смысловой реальности» М., 1999.
31. В.С.Степин «Теоретическое знание» Прогресс-Традиция, М., 2003.
32. Лейбниц Г.В. «Монадология» Сочинения, т.1, М.,1982.
33. Деррида Ж. «Письмо и различие» СПб, 2000
34. Цуккер А. «Пять лет Персимфанса» М., 1927.
35. Игнатьев М.Б., Ф.М. Кулаков, А.М. Покровский «Алгоритмы управления роботами-манипуляторами» первое издание – 1972, второе издание в США – 1973, третье издание 1977, Л., Машиностроение, 248 стр
36. Игнатьев М.Б., В.А. Мясников, А.М. Покровский «Программное управление оборудованием» первое издание – 1974, второе издание –1984, Л., Машиностроение, 540 стр..
37. Ястребов В.С., М.Б.Игнатьев, Ф.М. Кулаков, А.М. Покровский «Подводные роботы» Л., Судостроение,1977, 368 стр.
38. «Человек и робот» научно-популярный фильм, Леннаучфильм, авторы сценария М.Б.Игнатьев и Л.П. Клауз, 1980. Государственная премия СССР за 1982г
39. Игнатьев М.Б., Б.З.Ильевский, Л.П.Клауз «Моделирование системы машин» Л., Машиностроение, 1986, 304 стр.
40. Игнатьев М.Б.и др «Компьютерные игры» ,.Л, Лениздат, 1988, 168 стр.
41. Игнатьев М.Б., Тихомиров М.Е. «Внешнее управление самолетами и проблемы измерения» Вестник Северо-Западного филиала Метрологической Академии, вып.12, СПб, 2004, стр. 51- 66.
42. M.Ignatiev, N.Simatos, S.Sivasundaram “Aircraft as adaptive nonlinear system which must be in the adaptational maximum zone for safety” Proceedings of the First international conference on nonlinear problems in aviation and aerospace, Daytona Beach, Florida, USA, May 1996.
43. Игнатьев М.Б. «Роботы на основе нанотехнологий и пути перехода из одной мировой точки в другую» Вестник Северо-Западного отделения Метрологической академии, выпуск 2, Санкт-Петербург, 1998, стр.46-51.
44. Игнатьев М.Б. «Кибернетическая физика и пути перехода из одной мировой точки в другую» Материалы Х1 Всероссийской конференции по проблемам науки и высшей школы «Фундаментальные исследования и инновации в технических университетах» изд.Политехнического университета, Санкт-Петербург, 18-19 мая 2007г.стр.72-82.
45. M.B.Ignatyev “Semantics and selforganization in nanoscale physics” Abstract book of the 8 th International Conference on Computing Anticipatory Systems, Ed.D.Dubois, HEC-ULg, Liege, Belgium, August 6-11,2007, Symposium 6, p.18.
Издательство осуществляет публикацию основных научных результатов на соискание ученых степеней доктора и кандидата наук.
Журнал «Этносоциум» внесён в перечень ведущих научных журналов и изданий ВАК (Высшая Аттестационная Комиссия). Журнал зарегистрирован в Министерстве Российской Федерации по делам печати, телерадиовещания и средств массовых коммуникаций. Свидетельство о регистрации СМИ № 1047796682064
